Oracle’s Numbers
You are probably familiar with some of the data types supported by the Oracle Database for storing numeric values, but you might not be aware of the full range of types that it provides.
Some types (such as NUMBER, INTEGER) are provided for general use in SQL and PL/SQL, whereas others are only supported in PL/SQL (such as BINARY_INTEGER).
There are others (such as DECIMAL, REAL) that are provided to adhere to the SQL standard and for greater interoperability with other databases that expect these types.
Most of the numeric data types are designed for storing decimal numbers without loss of precision; whereas the binary data types (e.g. BINARY_FLOAT, BINARY_DOUBLE) are provided to conform to the IEEE754 standard for binary floating-point arithmetic. These binary types cannot store all decimal numbers exactly, but they do support some special values like “infinity” and “NaN”.
In PL/SQL you can define your own subtypes that further constrain the values that may be assigned to them, e.g. by specifying the minimum and maximum range of values, and/or by specifying that variables must be Not Null.
What do I prefer?
In my data models, I will usually use NUMBER to store numeric values, e.g. for quantities and measurements; for counts and IDs (e.g. for surrogate keys) I would use INTEGER (with the exception of IDs generated using sys_guid, these must use NUMBER).
In PL/SQL, if I need an index for an array, I will use BINARY_INTEGER (although if I’m maintaining a codebase that already uses its synonym PLS_INTEGER, I would use that for consistency). In other cases I will use INTEGER or NUMBER depending on whether I need to store integers or non-integers.
I don’t remember any occasion where I’ve needed to use FLOAT, or the binary types; and of the subtypes of BINARY_INTEGER, I’ve only used SIGNTYPE maybe once or twice. Of course, there’s nothing wrong with these types, it’s just that I haven’t encountered the need for them (yet).
What about Performance?
There are some differences in performance between these data types, but most of the time this difference will not be significant compared to other work your code is doing – see, for example, Connor on Choosing the Best Data Type. Choosing a data type that doesn’t use more storage than is required for your purpose can make a difference when the volume of data is large and when large sets of record are being processed and transmitted.
Reference Chart: Numeric Data Types
This diagram shows all the numeric data types supplied by Oracle SQL and PL/SQL, and how they relate to each other:
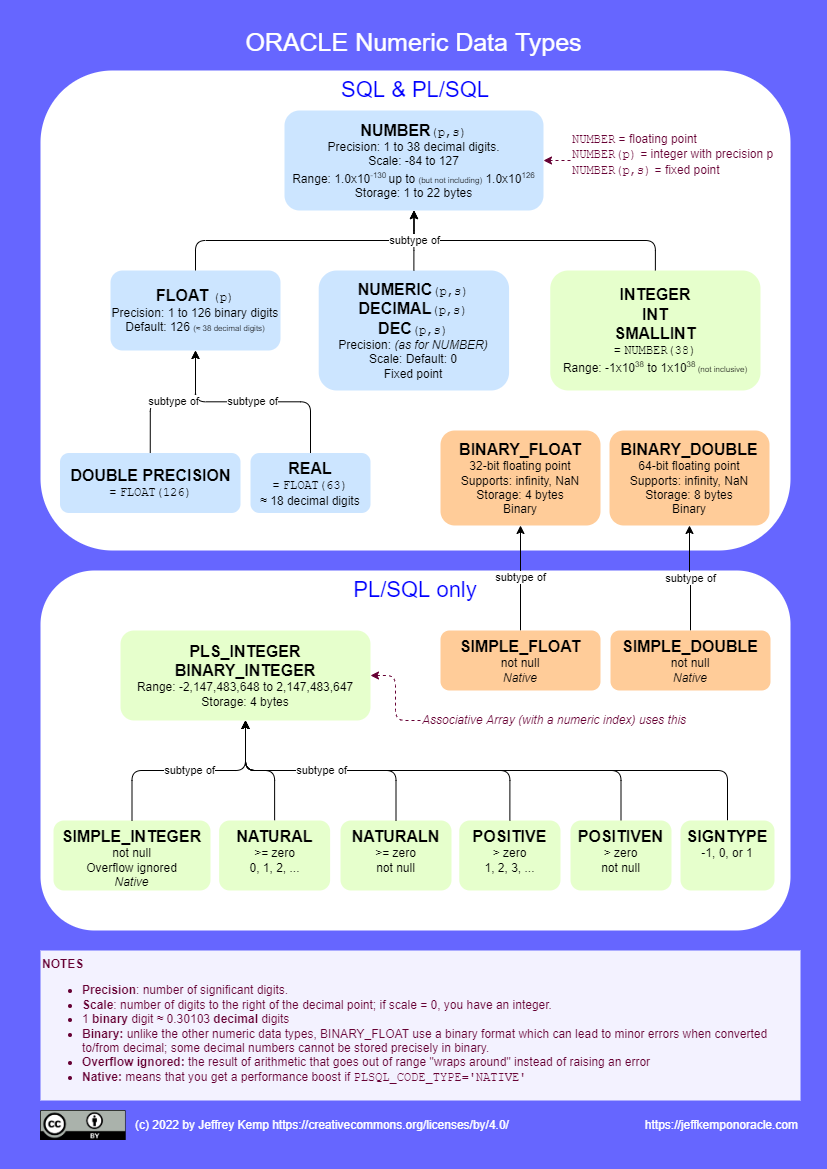
PDF version
Storing BIG Integers
From smallest to largest – the maximum finite integer that can be stored by these data types is listed here. It’s interesting to see that BINARY_FLOAT can store bigger integers than INTEGER, but NUMBER can beat both of them:
| BINARY_INTEGER | 2.147483647 x 109 |
| INTEGER | 9.9999999999999999999999999999999999999 x 1037 |
| BINARY_FLOAT | 3.40282347 x 1038 |
| NUMBER | 9.999999999999999999999999999999999999999 x 10125 |
| BINARY_DOUBLE | 1.7976931348623157 x 10308 |
To put that into perspective:
- If you need to store integers up to about 1 Billion (109), you can use a BINARY_INTEGER.
- You can use NUMBER to store:
- the estimated mass (in kilograms) of the observable universe (3 x 1052),
- the estimated total number of fundamental particles in the observable universe (1080), and
- Googol (10100)
- If you need to store Googolplex (10googol) or other ridiculously large numbers (that are nevertheless infinitely smaller than infinity), you’re “gonna need a bigger boat” – such as some version of BigDecimal with a scale represented by a BigInteger – which unfortunately has no native support in SQL or PL/SQL. Mind you, there are numbers so large that even such an implementation of BigDecimal cannot even represent the number of digits in them…
Storing SMALL Numbers
The smallest non-zero numeric value (excluding subnormal numbers) that can be stored by these data types is listed here.
| BINARY_FLOAT | 1.17549435 x 10-38 |
| NUMBER | 1.0 x 10-130 |
| BINARY_DOUBLE | 2.2250738585072014 x 10-308 |
These are VERY small quantities. For example:
- The size of a Quark, the smallest known particle, is less than 10-19 metres and can easily be represented by any of these types.
- You can store numbers as small as the Planck Length (1.616 × 10-35 metres) in a BINARY_FLOAT.
- But to store a number like the Planck Time (5.4 × 10-44 seconds), you need a NUMBER – unless you change the units to nanoseconds, in which case it can also be stored in a BINARY_FLOAT.
- I’m not aware of any specifically named numbers so small that they require a BINARY_DOUBLE; however, there are certainly use cases (e.g. scientific measurements) that need the kind of precision that this type provides.
